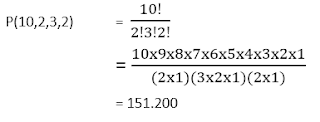Program Login Menggunakan Bahasa C

Pada kesempatan kali ini, saya akan membuat sebuah program login dengan bahasa C. Logika dari program yang akan dibuat adalah masukan Username dan Password, jika login berhasil, maka program akan memunculkan pesan berhasil. Jika login gagal sampai tiga kali, maka program akan berhenti. Berikut flowchartnya:

Dari flowchart di atas, dapat kita implementasikan kedalam bahasa C sebagai berikut:

#include<stdio.h>

#include<stdlib.h>

int main(){

   char username[8], pass[12];

   int repeat = 0, gagal = 0;

   while(repeat < 3){

      printf("Masukkan Username : ");

      scanf("%s", &username);

      printf("Masukkan Password : ");

      scanf("%s", &pass);

      if(strcmp(username,"login")==0 && strcmp (pass,"login123")== 0){

         printf("Selamat, kamu berhasil login\n");

         break;

      }else{

         printf("Input Salah!\n");

         gagal++;

         if(gagal == 3){

            printf("Sayang sekali, kamu tidak bisa login lagi\n");

         }

      }

      repeat++;

   }

   system("pause");

   return 0;

}

Setelah program dibuat, compile program.

Setelah itu, jalankan program dan hasilnya akan tampak seperti dibawah ini.

Jika program berhasil:

Jika program gagal:

Matematika Informatika - Prinsip Berhitung

1.       Jika terdapat 20 sarang merpati dan 41 ekor merpati,Berapakah banyak sarang yang ditempati 2 ekor merpati?

          a.       4

          b.      3 

          c.       2

          d.      1

Penyelesaian:

Maka akan  terdapat satu buah sarang yang berisi lebih dari 2 ekor merpati. Atau dengan menggunakan rumus diperoleh paling sedikit [ 41 / 20 ] =  1 sisa bagi. Maka aka nada merpati yang menempati 1 sarang yang sudah ditempati merpati lain.

2.       Dalam mata kuliah Algolirtma dan Pemograman diberikan tugas kelompok yang akan dibagi menjadi 6 kelompok. Jika terdapat 40 mahasiswa yang menempuh mata kuliah tersebut, berapakan jumlah mahasiswa yang menjadi anggota suatu kelompok yang sama?

a.       7

b.      8

c.       9

d.      10

Penyelesaian:

Anggoya himpunan mahasiswa daerah asal X dan kelompoknya sebagai anggota daerah kawan Y . Karena |X| = 40, |Y | = 7 dan [40/6] = 7.

Maka terdapat paling sedikit 7 anggota X yang dipasangkan dengan suatu anggota Y yang sama. Dengan demikian terdapat paling sedikit ada 11 mahasiswa yang menjadi anggota suatu kelompok yang sama.

3.       Tentukan permutasi atas semua unsur yang dapat dibuat dari kata-kata “ MATEMATIKA”!

a.        151211 Cara

b.       151399 Cara

c.        141344 Cara

d.       151200 Cara

Penyelesaian:

Pada kata “MATEMATIKA” terdapat 2 buah M, 3 buah A, dan 2 buah T yang sama sehingga permutasinya adalah :

     

4.       Hitunglah banyaknya kombinasi dari huruf – huruf a, b, c yang diambil 2 unsur !

a.        5

b.       4

c.        3

d.       2

Jawab :

5.       Ada berapakah kombinasi dari {a, b, c, d} sedemikian sehingga pengulangan diperbolehkan?

a.       25

b.      20

c.       15

d.      16

Penyelesaian:

Karena urutan dari anggota yang dipilih tidak diperhatikan, maka sebaiknya kita menulis kombinasi-3 tersebut dengan urutan menaik, untuk memastikan bahwa tidak adanya kombinasi yang sama ditulis lebih dari satu kali.

[a, a, a], [a, a, b], [a, a, c], [a, a, d], [a, b, b],

[a, b, c], [a, b, d], [a, c, c], [a, c, d], [a, d, d], 

[b, b, b], [b, b, c], [b, b, d], [b, c, c], [b, c, d],

[b, d, d], [c, c, c], [c, c, d], [c, d, d], [d, d, d]

Jadi, terdapat 20 kombinasi-3 dari {a, b, c, d} sedemikian sehingga pengulangan diperbolehkan.

Agar lebih mudah bisa menggunkan cara ini:

6.       Jika n adalah bilangan bulat positif, berapa banyaknya (i, j, k) yang mungkin apabila 1 ≤ i ≤ j ≤ k ≤ n?

Penyelesaian:

Sembarang tiga bilangan bulat berurutan (i, j, k) dapat direpresentasikan dengan n – 1 tanda garis dan 3 tanda silang, dengan posisi dari tanda silang mengindikasikan bilangan bulat positif mana yang dipilih dalam (i, j, k). Sehingga, berdasarkan teorema di atas, banyaknya urutan tiga bilangan bulat positif yang mungkin adalah

7.    Di dalam sebuah kelas ada 10 siswa yang gemar membaca, 15 siswa gemar menulis, dan ada 8 siswa yang gemar membaca & menulis. Berapa jumlah siswa di kelas tersebut ?

    |A U B| = |A| + |B| - |A ∩ B|

Penyelesaian:

Himp A = |A| = 10

Himp B = |B| = 15

|A ∩ B|  = 8

Jumlah          

   = |A U B|

   = |A| + |B| - |A ∩ B|

          = 10 + 15 – 8

          = 17

8.       Di Universitas Gunadarma terdapat mahasiswa/i yang memilih mata kuliah Matematika, Statistika, Komputer, Matematika & Statistika, Matematika & Komputer, Statistika & Komputer, serta Matematika & Statistika & Komputer, serta tidak memilih ketiga matkul tersebut.  Berikut adalah datanya :

Matematika                                             : 240 orang         

Matematika & Statistika                         : 76 orang

Statistika                                                 : 208 orang         

Matematika & Komputer                       : 48 orang

Komputer                                               : 160 orang         

Statistika & Komputer                           : 40 orang

Matematika & Statistika & Komputer  : 30 orang

Tidak mengambil ketiga matkul           : 70 orang

|A U B U C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|

Penyelesaian:

Matematika |A|          = 240                     |A ∩ C|               = 48

Statistika |B|               = 208                     |B ∩ C|               = 40

Komputer |C|             = 160                     |A ∩ B ∩ C|        = 30

|A ∩ B|                       = 76                      (A U B U C)       = matematika/statistika/komputer

|A U B U C|’              = 70

Jumlah mahasiswa

=  (A U B U C) U (A U B U C)’

= |A U B U C| + |A U B U C|’

= |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C| + |A U B U C|’        

          = 240 + 208 + 160 – 76 – 48 – 40 + 30 + 70

= 544

9.       Berapa banyaknya bilangan bulat antara 1 dan 100 yang habis dibagi 3 atau 5?

Penyelesaian:

Misalkan,

A = himpunan bilangan bulat yang habis dibagi 3

B = himpunan bilangan bulat yang habis dibagi 5

 A ∩ B = bilangan bulat yang habis dibagi 3 dan 5 ( yaitu himpunan bilangan bulat yang habis dibagi oleh KPK – Kelipatan Persekutuan Terkecil – dari 3 dan 5, yaitu 15)

Ditanyakan ?  | A ∪ B |

Jawab :

Pertama  kita harus mengitung

|A| = 100/3

= 33                       

|B| = 100/5

= 20                       

|A ∩ B| = 100/15

      = 6

Untuk mendapatkan

| A ∪ B |        = |A| + | B| - |A ∩ B|

= 33 + 20 – 6

= 47

Jadi ada 47 buah bilangan yang habis dibagi 3 atau 5

10.   Dalam sebuah kelas terdapat 25 mahasiswa yang menyukai matematika diskrit, 13 mahasiswa menyukai aljabar linier dan 8 orang diantaranya menyukai matematika diskrit dan aljabar linier. Berapa mahasiswa terdapat dalam kelas tersebut ?

Penyelesaian :

Misalkan A himpunan mahasiswa yang menyukai matematika diskrit dan B himpunan mahasiswa yang menyukai aljabar linier.

Misalkan,

A = 25

B = 13

Himpunan mahasiswa yang menyukai kedua mata kuliah tersebut dapat dinyatakan sebagai himpunan A ∩ B. Banyaknya mahasiswa yang menyukai salah satu dari kedua mata kuliah tersebut atau keduanya dinyatakan dengan |A υ B|. Dengan demikian,

|A υ B| =  |A|+|B| – |A ∩ B|

=  25 + 13 – 8

=  30.

Jadi, terdapat 30 orang mahasiswa dalam kelas tersebut.

Untuk format *.docx, silahkan klink link ini.